https://www.youtube.com/watch?v=M0Sa8fLOajA&list=PLE7DDD91010BC51F8&index=28
1. 복소수행렬
복소수로 구성된 벡터 z가 있습니다.

이것은 \(R^n\) 대신 복잡한 공간을 의미하는 \(C^n\)에 속합니다. z의 길이를 \(z^Tz\)로 생각할 수 있습니다. 그러나 그것은 옳지 않습니다. 예를 들어 z=(1,i)에서 길이가 0이 되기 때문입니다. 복소수의 경우 길이는 \(\bar{z}^Tz\)로 계산됩니다. \(\bar{z}^Tz\) 대신 \(z^Hz\)로 쓰고 H는 Hermitian으로 읽습니다. 복소수 행렬의 내적은 \(z^Hz\)입니다.
A는 복소수 행렬이고 대칭입니다. 지난 시간에 이야기한 좋은 매트릭스의 특성을 감안할 때 \(\바{A}^T=A\). 이것은 \(A^H=A\)로 쓸 수 있습니다.
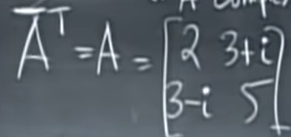
우리는 직교 행렬에 대해 Q \(Q^TQ=I\)가 성립함을 배웠습니다. Q도 복소수 행렬이면 \(Q^HQ=I\)이고 Q를 단일 행렬이라고 합니다.
2. 푸리에 행렬
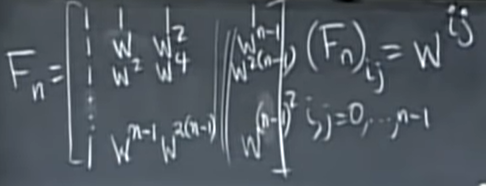
이것은 n x n 푸리에 행렬의 모양입니다. w는 복소수이고 \(F_n\)은 대칭 행렬입니다. w는 \(w^n=1\), 즉 \(w=e^{\frac{i2\pi}{n}}\)로 특징지어지는 특수한 숫자입니다. \(w=e^{\frac{i2\pi}{n}}\)는 복소평면상의 단위원으로 생각하면 이해하기 쉽다.
푸리에 행렬의 예를 살펴보겠습니다.
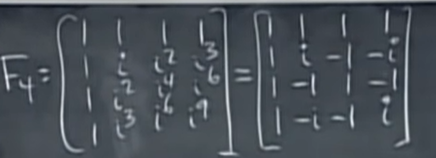
4×4 푸리에 행렬입니다. 이것은 4성분 벡터에 대한 4점 4점 푸리에 변환입니다. 푸리에 변환은 이 행렬 또는 그 역행렬을 곱하여 수행할 수 있습니다. 푸리에 행렬은 열이 서로 직교한다는 사실이 특징입니다. 따라서 정규 직교로 만들기 위해 적절한 숫자를 곱할 수 있습니다. 이 경우 \(F_4\)에 1/2을 곱하면 정규 직교가 됩니다. \(F_4\)의 모든 열은 직교이므로 \(F^HF=I\)가 유지됩니다. 따라서 \(F_4\)의 역행렬을 쉽게 얻을 수 있습니다.
다른 예를 살펴보겠습니다. \(F_{64}\)와 \(F_{32}\)의 관계는 무엇입니까? \(w_{64}\)는 단위원의 1/64입니다. \(w_{64}\)를 제곱하면 각도가 두 배가 되어 단위원의 1/32가 됩니다. \(w_{32}\)와 같은 위치에 있습니다. 따라서 \((w_{64})^2=w_{32}\). 이제 \(F_{64}\)와 \(F_{32}\)를 연결해 보겠습니다.

이 방정식에서 순열 행렬은 짝수 성분이 먼저 오고 홀수 성분이 나중에 오게 합니다. \(F_{64}\)를 제곱하면 최대 \(64^2\)까지 계산해야 합니다. 그리고 \(F_{32}\)는 \(F_{16}\)로 나눌 수 있습니다. 이와 같이 여러 단계를 거쳐 계산을 줄일 수 있습니다. 결과적으로 n x n 행렬의 빠른 푸리에 변환은 \(n^2\) 대신 \(\frac{1}{2}nlog_2(n)\)를 계산할 수 있습니다. (이 부분이 어려운듯…)